GÉOSTATISTIQUE

GÉOSTATISTIQUE

Pour des conditions économiques données, les réserves récupérables d’un gisement minier peuvent varier considérablement suivant la plus ou moins grande sélectivité de l’exploitation. Les contraintes géométriques, le support de la sélection, c’est-à-dire la taille des unités minimales que l’on peut sélectionner, et la structure de l’information disponible au moment de la sélection constituent des facteurs prépondérants. C’est pour prévoir leur effet et procéder à l’estimation des réserves récupérables que la géostatistique a mis au point ses modèles probabilistes. Dans les cas les plus simples, les méthodes linéaires connues sous le nom de krigeage se révèlent suffisantes et ne nécessitent rien de plus que la connaissance du variogramme du gisement. Par contre, il est souvent indispensable de recourir à des méthodes non linéaires pour évaluer les fonctions de récupération panneau par panneau et construire le paramétrage des réserves. Les techniques de simulation conditionnelle sont aussi largement utilisées. Enfin, il existe également une géostatistique non stationnaire, employée surtout en dehors du domaine strictement minier, notamment dans le domaine pétrolier.

Ressources et réserves récupérables

S’agissant d’un gisement minier, c’est-à-dire d’une accumulation géologique d’une substance utile que, pour abréger, nous appellerons métal, on doit très soigneusement distinguer les notions de ressources et de réserves. Par ressources, on entend la quantité totale de métal contenue dans le gisement géologique, que cette quantité soit ou non économiquement exploitable. Les réserves, au contraire, représentent cette fraction des ressources qu’il est techniquement possible et économiquement utile de récupérer. Alors que les ressources constituent une caractéristique purement géologique du gisement, les réserves récupérables résultent de l’impact d’une activité humaine (technico-économique) sur un phénomène naturel. Il s’agit donc d’une notion essentiellement relative: les réserves récupérables dépendent étroitement des conditions économiques et techniques du moment. Elles augmenteront, souvent de manière très substantielle, si le cours du métal s’élève ou si les techniques d’exploitation et de traitement s’améliorent; elles diminueront au contraire si le coût de la main-d’œuvre ou de l’énergie subit une augmentation. À ces effets, évidents et bien connus, s’en ajoutent d’autres, de caractère plus technique mais non moins importants, que nous rangerons sous trois rubriques: contraintes géométriques, support de sélection et structure de l’information.

Contraintes géométriques

Pour des raisons évidentes, la forme d’une excavation ne peut être quelconque, mais doit respecter des contraintes sévères, qui dépendent d’ailleurs étroitement du procédé technologique d’exploitation utilisé. Dans une exploitation à ciel ouvert, par exemple, le contour de la carrière doit respecter la pente d’équilibre naturel. Dans une formation stratiforme, on s’imposera souvent de n’extraire qu’une seule passée, d’épaisseur supérieure à un minimum donné. Dans certains cas (exploitation souterraine, formation stratiforme peu profonde), on peut, en première approximation, considérer le volume total à excaver comme la réunion d’unités (relativement grandes) ou panneaux, V¹, V², etc., dont chacun peut, à volonté, être extrait ou laissé en place indépendamment des autres. Par suite de ces contraintes géométriques, il arrive presque toujours que des portions riches, mais isolées, du gisement doivent être abandonnées, les frais d’accès étant trop élevés. Inversement, on est souvent contraint d’extraire des passées pauvres intercalées dans les zones riches.

Support de sélection

À l’intérieur du volume de l’excavation, ou d’un panneau donné V, on peut souvent procéder à une sélection. Considérant V comme la réunion d’unités élémentaires jointives plus petites, ou blocs, v¹, v², etc., chacun de ces blocs v pourra être envoyé, après son extraction, soit au minerai soit au stérile. Le support de cette sélection, c’est-à-dire la taille des blocs v, exerce une influence considérable sur les réserves récupérables, qui peuvent en certains cas varier du simple au double si le support v passe de plusieurs milliers à quelques dizaines de mètres cubes. Entre une exploitation en grandes masses, donc bon marché mais peu sélective, et une exploitation assurée par des engins plus petits et plus mobiles, permettant donc une meilleure récupération, mais à un coût plus élevé, le choix doit évidemment se fonder sur des critères économiques.

Structure de l’information

L’information disponible au moment où seront effectivement prises les décisions aux différents niveaux (choix de panneaux à extraire, sélection des blocs, etc.) sera parfois abondante, lors de la sélection des blocs, si l’on dispose des résultats d’analyse des trous de tir à maille serrée (par exemple 10 m 憐 10 m), plus pauvre en général lors du choix des panneaux, où l’on ne disposera que des résultats de sondages de reconnaissance à plus grande maille (par exemple 100 m 憐100 m), mais en aucun cas on ne connaîtra les valeurs exactes des caractéristiques des unités que l’on sélectionne. Par suite de ces erreurs d’estimation, on enverra au stérile un certain nombre de blocs riches, sous-estimés, et inversement. De même, on abandonnera certains panneaux qui auraient été rentables, et on en retiendra d’autres qui se révéleront décevants.

La structure de cette information exerce donc une influence importante sur les réserves qui seront effectivement récupérées. En ce qui concerne l’estimation, ou la prévision, de ces réserves, on doit très soigneusement distinguer l’information actuelle (disponible au moment où l’on procède à l’estimation: par exemple, la maille de reconnaissance 100 m 憐 100 m) et l’information ultime, qui ne sera disponible qu’au moment de la sélection des blocs (par exemple les trous de tir à maille 10 m 憐 10 m).

Ce décalage entre information actuelle et information future est la source de l’une des principales difficultés de l’estimation des réserves récupérables. Comme la sélection ultime sera effectuée sur la base d’une information non encore disponible, on ne peut pas prévoir à l’avance son effet sans anticiper, en probabilité, cette information future sur la base de l’information actuelle.

C’est avant tout pour essayer de prévoir l’influence de ces divers facteurs (contraintes géométriques, effets de support et d’information) sur la détermination des réserves récupérables et les conditions de leur estimation (à partir d’une information fragmentaire) que se sont développés, depuis les années 1950, un certain nombre de modèles probabilistes dont l’ensemble constitue la géostatistique. Cette discipline a d’ailleurs aujourd’hui assez largement débordé son cadre minier originel et rencontré de nombreuses et fructueuses applications dans d’autres domaines: géologie pétrolière, sylviculture, météorologie, géophysique, cartographie, travaux publics...

Le paramétrage technique des réserves

Comme les réserves d’un gisement dépendent de nombreux facteurs techniques et économiques, l’exploitant a le choix entre un nombre en général assez élevé d’options possibles. Pour l’aider à faire son choix, la géostatistique se propose de disjoindre le problème de la recherche du meilleur projet en deux parties, l’une purement technique, l’autre économique. La première partie constitue le paramétrage technique des réserves récupérables. Elle consiste à sélectionner, en fonction d’un ou deux paramètres purement techniques (par exemple des teneurs de coupure), une famille de projets optimaux en un sens purement technique, c’est-à-dire indépendamment des facteurs économiques. Cette famille possède la propriété suivante: quelles que soient les conditions économiques du moment (cours des métaux, prix de revient de l’extraction et du traitement, etc.) et la formule de valorisation, le projet économiquement optimal, quel qu’il soit, tombe nécessairement à l’intérieur de cette famille d’optimums techniques.

Cette disjonction, ou paramétrage technique préalable, n’est pas toujours possible en toute rigueur, mais souvent réalisable en première approximation. Considérons par exemple le cas simple où la valeur d’un projet est une fonction B(Q,T,V) de trois variables: la quantité Q de métal récupéré, le tonnage T de minerai à traiter, enfin, le volume total V à extraire (minerai + stérile).

Il n’est pas nécessaire de connaître cette fonction B pour paramétrer les réserves. Il suffit de supposer (ce qui est raisonnable) que B est une fonction croissante de Q et décroissante de T et V. Le paramétrage est alors possible. De fait, parmi tous les projets techniquement possibles comportant le même tonnage traité T et le même volume extrait V, le meilleur est forcément celui qui maximise la quantité de métal Q.

On définira donc, en fonction de T et de V, le projet qui maximise Q (ou plutôt son estimation) et on construira la fonction correspondante Q = Q(T,V), qui réalise le paramétrage cherché. Pour choisir le projet économiquement optimal, une fois connue la fonction B, il ne reste plus en principe qu’à déterminer les valeurs de T et V qui maximisent B[Q(T,V),T,V]. En pratique, au lieu de T et de V, on utilise le plus souvent deux autres paramètres ayant le sens de teneurs de coupure. La figure 1 présente la situation dans un cas typique où le recours à des méthodes non linéaires est obligatoire.

Dans certains cas plus simples, en l’absence de sélection au niveau des blocs par exemple, une technique linéaire appelée krigeage (ainsi nommée d’après son promoteur, D. G. Krige) se révèle suffisante. Historiquement, les méthodes linéaires étaient déjà opératoires au cours des années soixante, tandis que la géostatistique non linéaire, d’ailleurs encore en cours d’évolution, a été élaborée après 1970.

La géostatistique linéaire

La répartition spatiale des teneurs dans un gisement se présente sous un aspect partiellement aléatoire et partiellement structuré. L’étude géologique permet de définir la structure qualitative de la minéralisation et constitue un préalable indispensable pour la géostatistique. Mais, en raison du caractère trop erratique, surtout au niveau local, de la variabilité des teneurs, la géologie ne permet pas, en général, de prévisions quantitatives déterministes. Inversement toutefois, on ne peut nullement assimiler ces teneurs à des variables aléatoires indépendantes. Heureusement d’ailleurs pour l’industrie minière: si les teneurs étaient indépendantes, aucune exploitation sélective ne serait possible. La situation réelle se trouve à mi-chemin de ces deux extrêmes. Les modèles de la géostatistique assimilent les teneurs aux différents points du gisement à des variables aléatoires plus ou moins fortement corrélées, et c’est justement la plus ou moins grande intensité de ces corrélations qui reflète, dans le modèle, la plus ou moins grande continuité du phénomène physique réel.

Pour exprimer ces corrélations, la géostatistique utilise une fonction 塚(h ) appelée variogramme , qui représente, en fonction du vecteur h , la moitié de la valeur moyenne du carré de la différence des teneurs z (x ) et z (x + h ) observées aux points x et x + h . En termes probabilistes, les teneurs z (x ) sont interprétées au moyen de variables aléatoires Z(x ); le variogramme 塚(h ) est de même interprété comme une espérance mathématique, soit:

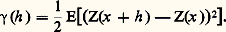Concrètement, 塚(h ) représente en fonction de h la manière plus ou moins rapide dont se dégrade l’«influence» d’un échantillon donné sur des zones de plus en plus lointaines du gisement.

Le modèle probabiliste correspondant est celui des fonctions aléatoires intrinsèques (c’est-à-dire à accroissements stationnaires), plus général et mieux adapté aux réalités minières que celui des fonctions aléatoires stationnaires. C’est pourquoi la géostatistique utilise les variogrammes plutôt que les fonctions de covariance, par rapport auxquelles ils présentent aussi de sérieux avantages du point de vue de leur estimation (ou inférence statistique). Il n’est d’ailleurs pas nécessaire de supposer le variogramme 塚(h ) constant dans l’espace du gisement tout entier. On peut admettre qu’il se déforme lentement d’une zone à l’autre. On obtient ainsi un modèle (fonction aléatoire localement intrinsèque) suffisamment souple pour s’adapter à la quasi-totalité des situations rencontrées dans la pratique minière (dans d’autres domaines, par exemple en géostatistique pétrolière, ce modèle peut se révéler insuffisant, et il existe toute une géostatistique non stationnaire).

La figure 2 présente la technique d’estimation linéaire appelée krigeage. Le but réel du krigeage n’est d’ailleurs pas tellement de minimiser la variance d’estimation, mais surtout d’éviter la surestimation systématique des panneaux riches. Compte tenu de l’effet de support, les teneurs des panneaux ont toujours une dispersion plus faible que celles des échantillons. Il en résulte qu’à un échantillon riche correspond un panneau moins riche en moyenne que son échantillon. En tenant compte de l’influence des échantillons extérieurs, le krigeage corrige l’effet de cette très grave cause d’erreur systématique. La figure 3 présente quelques types de variogrammes. Le tableau ci-dessous indique comment la géostatistique linéaire rend compte de l’effet de support et de l’effet d’information.

La géostatistique non linéaire

Dès qu’il y a sélection et que l’information ultime n’est pas encore connue, les méthodes linéaires ne suffisent plus pour estimer les fonctions de récupération et paramétrer les réserves (fig. 1); on doit recourir à la géostatistique non linéaire. Considérons par exemple l’effet de support. Ce n’est plus seulement la variance des teneurs Z(v) des blocs v, mais leur loi de distribution que l’on veut déterminer à partir de celle des teneurs Z des échantillons quasi ponctuels. On utilise pour cela la technique des anamorphoses gaussiennes: il existe toujours deux variables gaussiennes réduites Y et Y^v et deux fonctions croissantes 﨏 et 﨏^v telles que Z = 﨏(Y) et Z(v) = 﨏^v (Y^v). La fonction 﨏 est connue expérimentalement, et on cherche à déterminer la fonction 﨏^v (qui permet de reconstituer la loi des blocs).

Supposons que Z = 﨏(Y) soit la teneur d’un point x choisi au hasard dans le bloc v. Comme Z(v) est, par définition, la moyenne des teneurs des points x de v, l’espérance conditionnelle de Z à Z(v) fixé est toujours égale à Z(v). On a donc:

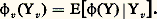Si, de plus, on admet (en première approximation) que la loi à deux variables (Y,Y^v) est gaussienne, avec un coefficient de corrélation r , on en déduit que 﨏^v est de la forme:

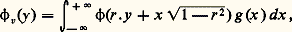g étant la densité de la loi de Gauss réduite. On adopte pour r la valeur qui donne la valeur correcte pour la variance S²(v) des blocs v (que l’on sait calculer à partir du variogramme, cf. tableau).

En pratique, il est commode d’introduire des développements en polynômes d’Hermite:

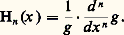Si le développement de 﨏 est:

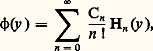celui de 﨏^v sera:

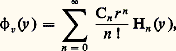et la variance de Z(v) s’en déduit par:

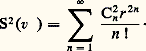Connaissant S²(v) et les coefficients Cⁿ , cette relation permet de déterminer r . Ce modèle (il en existe d’autres) conduit en général à une bonne prévision de la loi des blocs, pourvu que v ne soit pas trop grand.

Une formulation analogue permet de construire les lois à deux variables (teneur du bloc et de son estimation ultime) conditionnées par l’information actuelle et d’en déduire les fonctions de récupération. Ces calculs, assez complexes, sont grandement simplifiés par le recours à la méthode dite du krigeage disjonctif.

Enfin, de nombreux problèmes, trop complexes pour être résolus par le calcul, nécessitent le recours aux simulations conditionnelles. Il s’agit de modèles numériques de gisements fournissant des valeurs numériques z (x ) en chaque point x d’une maille serrée (en pratique, souvent plusieurs centaines de milliers de points), respectant le variogramme et l’histogramme des teneurs réelles ainsi que les valeurs expérimentalement connues aux points où des échantillons ont été prélevés. Ces modèles permettent aux praticiens de simuler une exploitation réelle et de prévoir, par exemple, l’influence régulatrice d’un stockage intermédiaire, ou d’une combinaison de plusieurs chantiers, sur la fluctuation des teneurs à l’entrée de l’usine de traitement. La géostatistique se révèle ainsi de plus en plus indispensable, non seulement pour définir et estimer les réserves, mais également pour assurer la planification et le contrôle à moyen ou long terme d’une exploitation en cours.

● géostatistique nom féminin Science basée sur une généralisation de la théorie des probabilités et appliquée à des problèmes d'estimation des teneurs ou de la puissance d'un gisement.

Encyclopédie Universelle. 2012.